Betting On Death

A Cowboy’s Charm

Let’s imagine, for the sake of argument I hope, that you’ve got no friends, no family - no one to send a letter to even if you wanted. You ride alone through open country, breaking broncos and sleeping under God’s ceiling, a true lone ranger.

As you’re going about your regrettably very lonely day, you happen across a strange man with a strange proposition:

“I’ll bet you’re dead within the year,” he says.

Now, being the street-smart smooth talker that you are, you immediately shoot the man clean through the jaw, since he’s obviously planning to kill you.

But as you go to light your cigarette with a gusto befitting your guile, you think, “Wait - that was actually a really good bet! I’m an idiot. No wonder I ride alone. I just know I’ll end up some nameless withered scrap of leather and bone, mourned only by tumbleweeds and dust out on the prairie.”

It’s alright partner, we all have those thoughts from time to time.

But what would happen if we took the straggler’s proposition a bit more seriously?

This, believe it or not, is going to be a post about financial economics.

The Basics

Let’s ignore the obvious moral hazard involved in giving someone a large financial incentive to kill you for a moment by imagining our bet is completely anonymous and part of a large, globally diversified pool.

If you take a first-person point of view, the utility calculus is simple:

• If I die, I’m dead. I don’t feel loss. No one cares (I’m a lone ranger).
• If I survive, I get upside.
• Therefore, from my perspective there’s only upside.

Ok, cool thought experiment, but so what? Right? Wrong. Stay with me.

The mechanics:

• The “long life” folks buy a life token that pays $\(1\) if they are alive at time \(T\). In doing so, they issue a complementary death token (charming, I know) purchased by their “long death” counterparty which pays $\(1\) if they are dead at \(T\).
• Exactly one of these pays out, so the system is effectively a discount bond chopped into two pieces, since the combined payoff is \(X_L + X_D = 1\).

What’s the counter-intuitive result? Everyone can have positive excess returns, conditional on being alive to collect them.

The Proof And The Pudding

Let me back up this fantastical claim.

Since the combined position is risk-free, the tokens’ combined price is \(\pi_L(T)+\pi_D(T) = e^{-rT}\) and if mortality is diversifiable and largely independent of the market discount factor, we can price the tokens actuarily according to the survival probability \(p(T)\) giving:

Which gives us the gross return distributions as:

We can easily see that the expected return for each is simply the risk-free rate, as expected, but the distributions have some very interesting properties that obscured by this fact. Let’s do an example, with \(r = 3\%\), \(p(T) = 98\%\), and \(T = 1\).

Conditional on being alive to collect, being long life provides a guaranteed return of \(\frac{e^{0.03}}{0.98} - 1 = 5.15\%\), or an excess return of \(2.15\%\). Not bad at all - when compounded this would amount to a \(2 \times\) higher return over 35 years. If you had no one to write a letter to even if you wanted, would you take that bet?

On the ghoul side of the coin, the TLDR is that it’s a massively right-skewed asset with negative median return. The interesting part is what happens when you continue rolling this until death finally comes to collect. Assuming the lifer entirely reinvests their wealth \(W\), the deathlord’s bet size grows as \(B_i = W_{0} \times (1.0515)^{i} \times \tfrac{0.02}{0.98}\). This is exponential but is ultimately bounded by the human lifespan, so the total capital outlay is bounded by \(\sum B_i \lesssim 4.715 \times W_0\) assuming a maximum betting life of 50 years.¹

Needless to say, with a return of approx. \(\frac{e^{0.03}}{0.02} - 1 = 5,052.3\%\) on the last bet, even a mom-and-pop death lover’s cooperative could afford to lose money for a lifetime and still come out well ahead. Literally. Moreover, by embedding a small risk premium death and co. could also obtain an unconditional expected excess return from a portfolio of these bets, while leaving a portion the lifers’ intact, as long as the risk premium is smaller than \(2.15\%\).

And this, my friends, is magic — the golden goose, lunch so free it almost hurts…

Frankenstein’s Frankincense

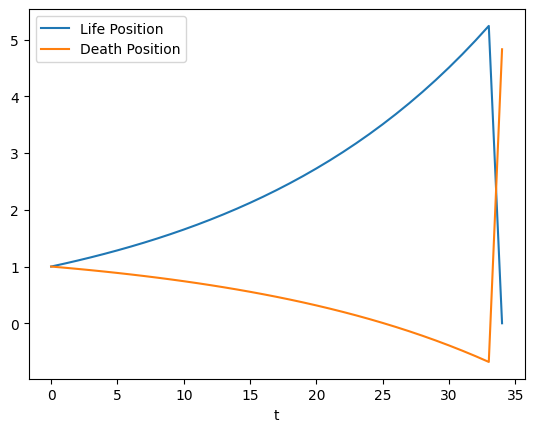
A typical path.

I've created a monster.

Frankenstein’s free lunch comes at a cost:

As volume grows in this pool, killing people at random becomes statistically profitable. The mere existence of this market would create an incentive for diffuse, probabilistic violence.

To be absolutely clear: this should not exist.²

This would not only create possibly the worst incentive known to man, and be useless to anyone with loved ones, it would also be the terminal financialisation of life itself.

As ChatGPT would say:

Capital no longer needs labor. It just needs you to keep existing long enough for the yield curve to roll over. And if not? It claims your remainder. The logic is airtight.

We did a fun thought experiment. We got to do absurdist comedy, we got to do financial engineering, and we got to discuss the commonly underappreciated fact that utility is implicitly conditioned on consciousness.

But I’ll say it again - do not do this!!!

I came up with it, and I’m telling you I don’t want you to do it so you have to listen.

Otherwise I’m taking my ball and going home.

Fin

I hope you’ve had fun building excess returns from qualia alone with me, the punchline is that free lunch exists only for those with no one to leave the bill to.³

That being said: don’t do this!!!

Thanks for reading.