Poker Hand Equity Is Intransitive
Published:
Let’s show the counterintuitive fact that poker hands themselves are intransitively ordered by pure preflop equity.
Note: the exact equity file comes from https://raw.githubusercontent.com/girving/poker/master/exact.txt.
Plots
def plot_heatmap(hands, equity, order):
n = len(order)
M = np.full((n, n), np.nan)
# Only fill the upper triangle to avoid mirrored duplicates
for i, h1 in enumerate(order):
for j, h2 in enumerate(order):
if i < j and h1 != h2:
M[i, j] = equity[(h1, h2)] - 0.5
plt.figure(figsize=(9, 9))
cmap = plt.get_cmap("RdBu").copy()
cmap.set_bad(color="white")
plt.imshow(M, cmap=cmap, vmin=-0.1, vmax=0.1)
plt.colorbar(label="Equity - 0.5")
plt.title("Pairwise Equity Heatmap (Upper Triangle)")
plt.xlabel("Opponent")
plt.ylabel("Hero")
plt.show()
def plot_equity_surface(hands, equity, zlim=0.35):
avg = avg_equity(hands, equity)
order = sorted(hands, key=lambda h: avg[h], reverse=True)
n = len(order)
Z = np.zeros((n, n))
for i in range(n):
for j in range(n):
if i == j:
Z[i, j] = 0.0
else:
Z[i, j] = equity[(order[i], order[j])] - 0.5
surface = go.Surface(
z=Z,
colorscale="RdBu",
cmin=-zlim,
cmax=zlim,
showscale=True,
colorbar=dict(title="Equity − 0.5"),
)
plane = go.Surface(
z=np.zeros_like(Z),
showscale=False,
opacity=0.18,
colorscale=[[0, "black"], [1, "black"]],
)
fig = go.Figure(data=[surface, plane])
fig.update_layout(
title="Preflop Equity Surface (Full Matrix)<br>"
"z = equity − 0.5, ordered by average equity",
scene=dict(
xaxis_title="Opponent rank (strong → weak)",
yaxis_title="Hand rank (strong → weak)",
zaxis_title="Equity − 0.5",
aspectmode="manual",
aspectratio=dict(x=1, y=1, z=0.55),
camera=dict(eye=dict(x=1.6, y=1.6, z=0.8)),
),
width=1000,
height=900,
margin=dict(l=20, r=20, t=70, b=20),
)
fig.show()
def find_best_intransitive_cycle(hands, equity):
wins = {a: [b for b in hands if a != b and equity[(a, b)] > 0.5] for a in hands}
best = None
best_score = -1.0
for a in hands:
for b in wins[a]:
for c in wins[b]:
if c == a or c == b:
continue
if equity[(c, a)] > 0.5:
margins = [
equity[(a, b)] - 0.5,
equity[(b, c)] - 0.5,
equity[(c, a)] - 0.5,
]
score = min(margins)
if score > best_score:
best_score = score
best = (a, b, c)
return best, best_score
def plot_intransitive_cycle(hands, equity):
cycle, score = find_best_intransitive_cycle(hands, equity)
if not cycle:
print("No intransitive 3-cycle found.")
return
a, b, c = cycle
G = nx.DiGraph()
edges = [(a, b), (b, c), (c, a)]
for u, v in edges:
G.add_edge(u, v, weight=equity[(u, v)])
pos = nx.circular_layout(G)
plt.figure(figsize=(6, 6))
nx.draw_networkx_nodes(G, pos, node_color="#1f77b4", node_size=1800, alpha=0.9)
nx.draw_networkx_labels(
G, pos, font_color="white", font_size=11, font_weight="bold"
)
nx.draw_networkx_edges(
G,
pos,
arrowstyle="-|>",
arrowsize=20,
width=2.2,
edge_color="#333333",
connectionstyle="arc3,rad=0.10",
)
edge_labels = {(u, v): f"{equity[(u, v)]:.3f}" for u, v in edges}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=10)
plt.title(f"Intransitive cycle (min margin {score:.3f}) {a} > {b} > {c} > {a}")
plt.axis("off")
plt.show()
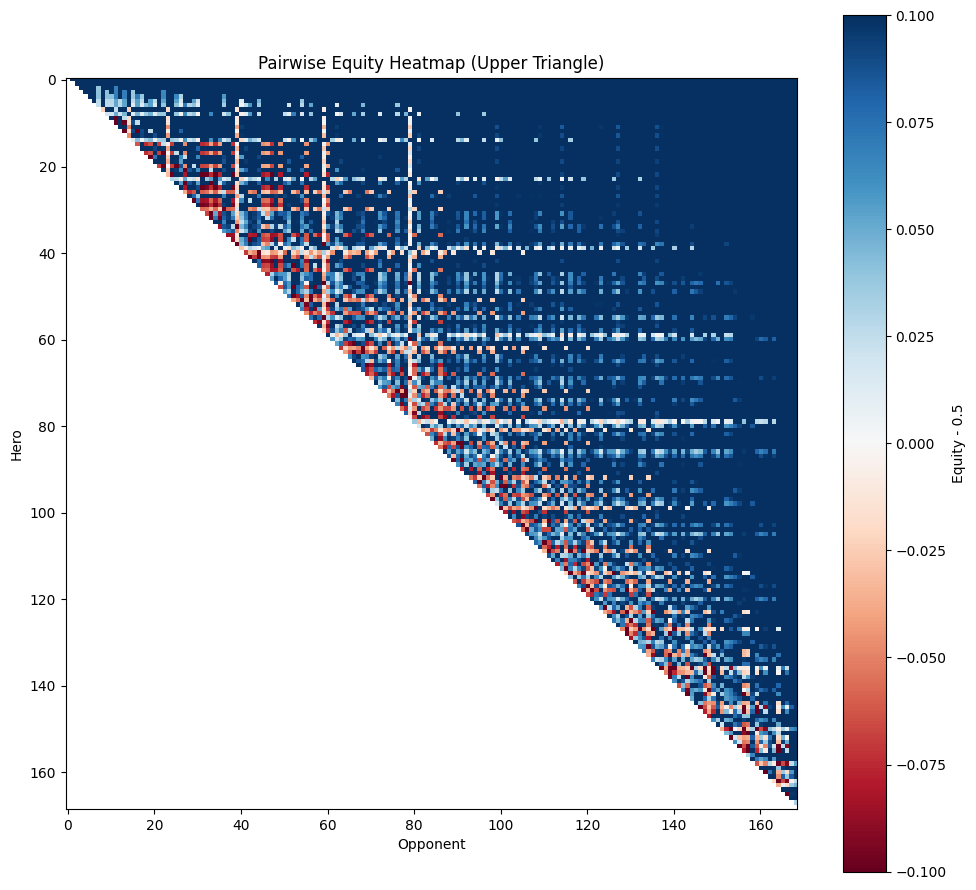
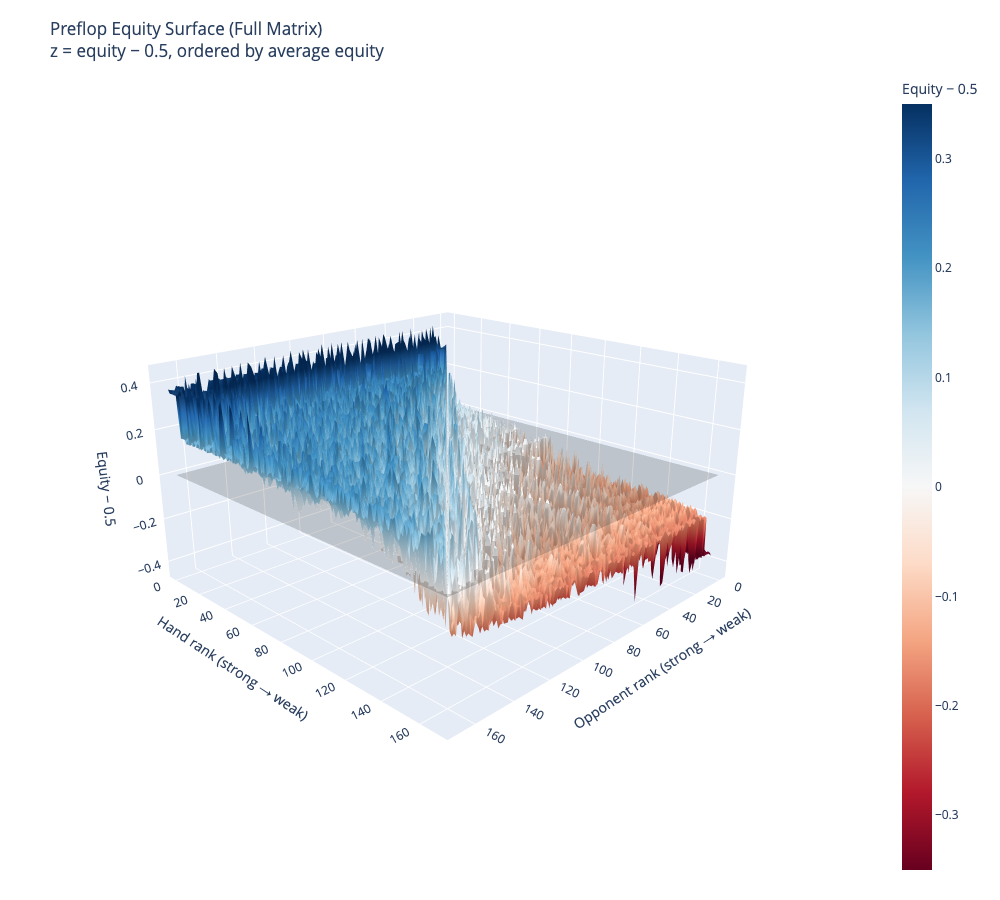
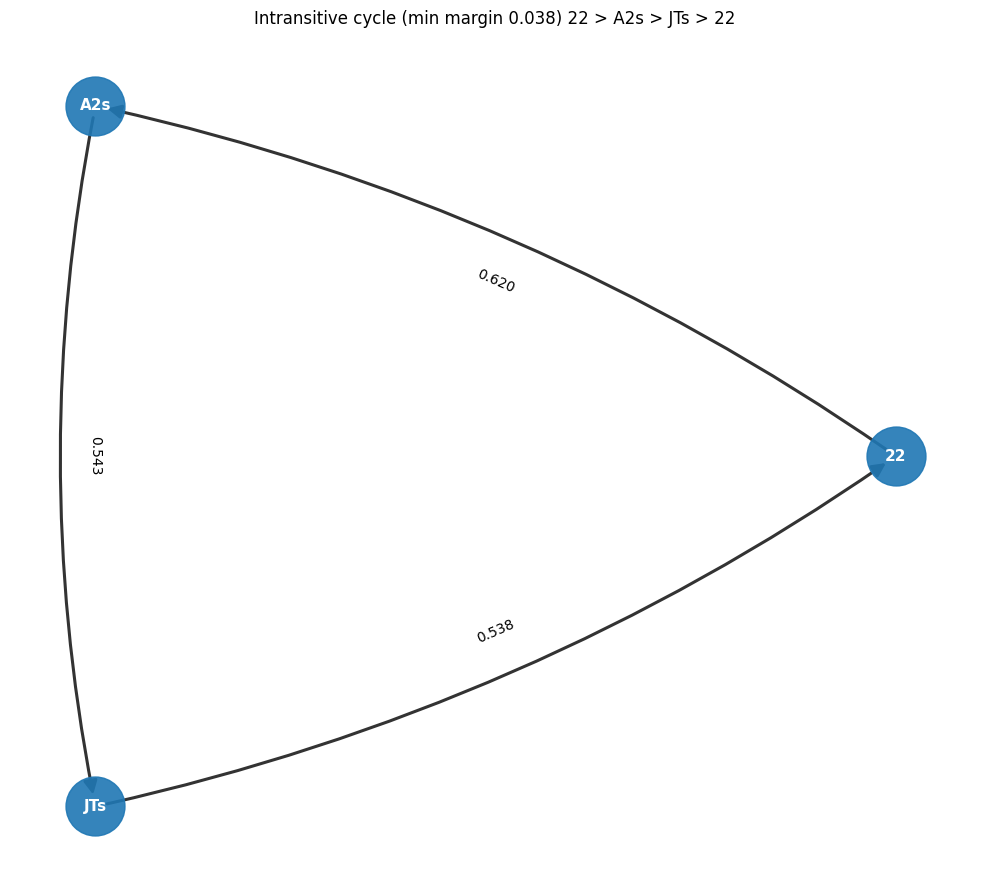
Pairwise, equity rankings are not a monotonic ordering!


